Posterior Sampling via Autoregressive Generation

Bridging Generative Sequence Modeling and Online Decision-Making

Real-world decision-making often involves grappling with uncertainty. This challenge is particularly acute in areas like recommendation systems, where new items are continuously introduced, and personalized user experiences where new individual consistently enter the system. Traditional bandit algorithms struggle to handle the complex, unstructured data (e.g., text and images) that are common in modern applications. This work introduces a novel framework for learning bandit algorithms using autoregressive sequence models, offering a scalable and principled approach to Thompson sampling.

Problem Setting

Formally, we define meta-learning bandit problem where the bandit repeatedly encounters new tasks that require exploring to gather useful information. We illustrate our approach using a news article recommendation setting.

Each day, new articles (actions) are released, and the system needs to recommend these to users while balancing exploration (trying new articles) and exploitation (showing the articles predicted to be the most popular based on the article headline text). Although article headlines provide a useful early indicator of article performance, models that solely rely on such features will eventually be outperformed by simple alternatives that learn from actual user feedback. The algorithm also has access to a large historical recommendation dataset on previously released articles from past days.

Our meta-bandit setting has two stages: (1) learning from a massive historical dataset and (2) online decision-making on a new task (recommendation problem with new items).

Our Approach

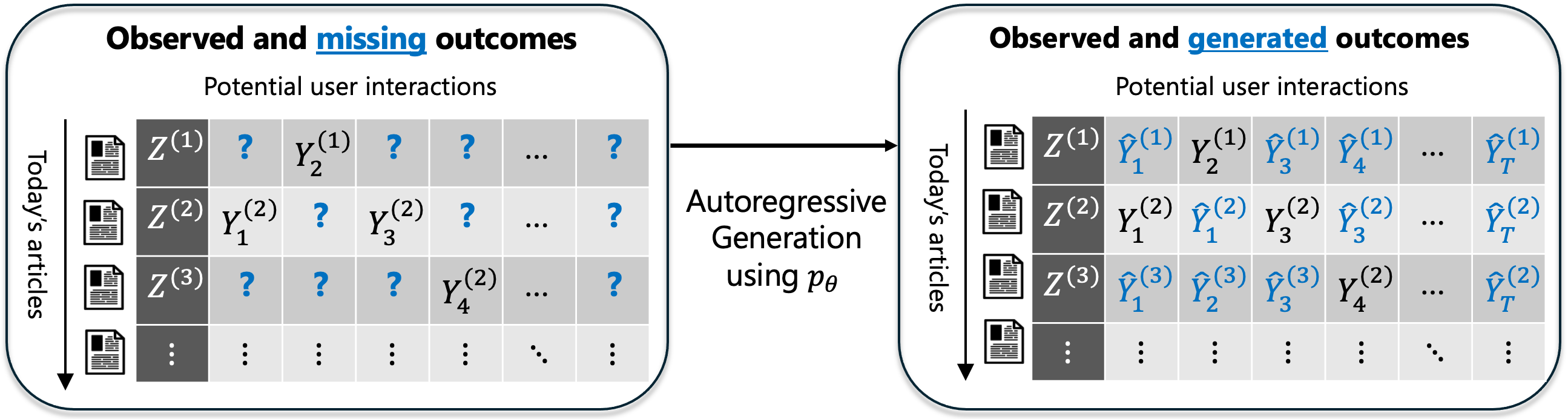
The impetus of our approach is that unobserved outcome data is the source of the decision-maker’s uncertainty: feedback on an article has only been gathered from a subset of users, and there is residual uncertainty in how others users would respond.

We view uncertainty about unobserved outcomes as the source of uncertainty, avoiding explicit reference to latent parameters or variables. Calibrated generation (imputation) of missing outcomes enables uncertainty quantification and decision-making.

Specifically, we propose a two-phase approach:

(1) Pretraining: Use the historical recommendation data to train an autoregressive sequence model $p_\theta$ that predicts successive user responses (e.g., clicks) to an article. This sequence model also takes in the article headline as input (via a pre-trained LLM that is fine-tuned).

(2) Online Decision-Making: At decision time, we use the pretrained model to autoregressively sample (impute) imaginary sequences of user feedback for each article. We then choose the article with the highest average imputed reward, representing a sample from the posterior distribution of the article’s true average reward.

Posterior Sampling via Autoregressive Generation (PS-AR). PS-AR uses autoregressive generation (imputation) of unobserved potential outcomes to (implicitly) reason about uncertainty and drive exploration of arms that could plausibly be optimal. After imputing all missing outcomes, it forms an imputed mean reward per action and selects the action with the highest imputed mean.

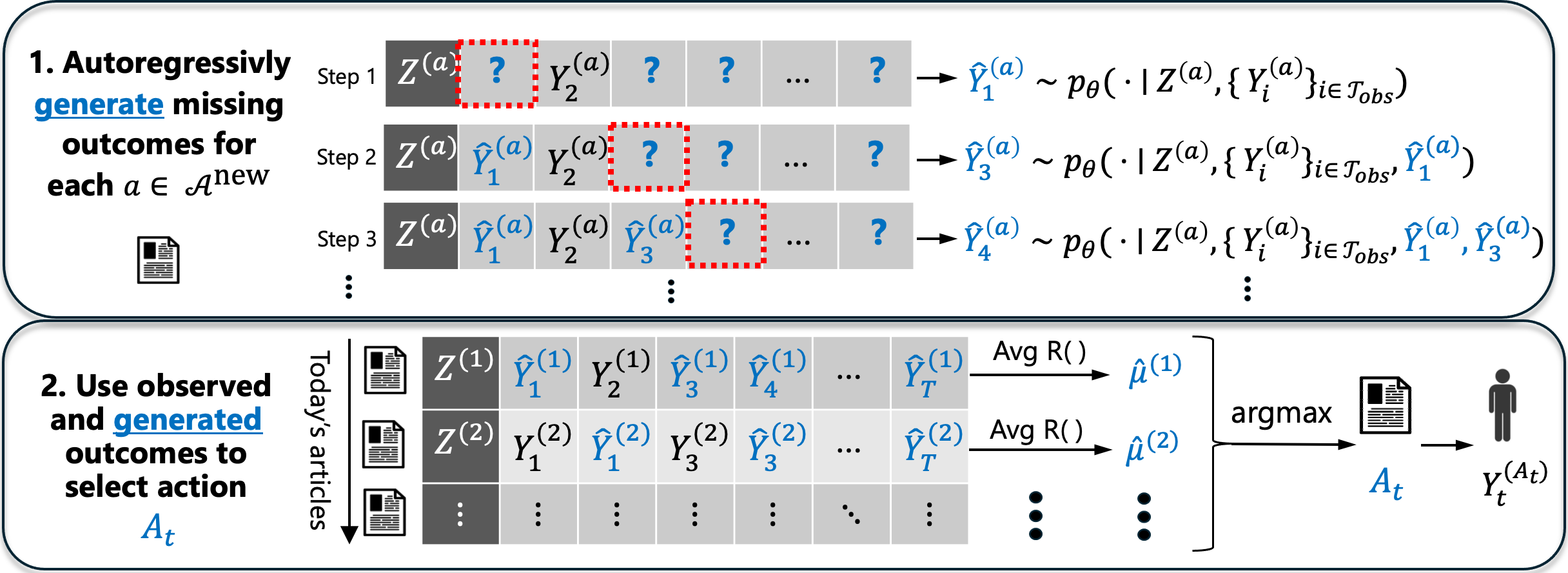
Key Insights:

• Implementation of Thompson Sampling: We show that this Posterior Sampling via Autoregressive Generation approach is a principled implementation of Thompson sampling (with a learned prior), a powerful algorithm for balancing exploration and exploitation.
• Regret Bound: We prove a novel regret bound that links the online performance of our algorithm to the prediction loss of the pretrained sequence model. This provides a strong theoretical foundation for our approach.
• Pretraining as Empirical Bayes:: We show that for particular choices for sequence model classes minimizing our pretraining loss is equivalent to maximizing the marginal likelihood, the criterion that is used in Empirical Bayes, a popular approach to fitting a prior distributions to observed data. We find in experiments that training on our sequence loss can recover the true Bayesian prior. Our pretraining procedure can be viewed as learning an approximate Bayesian model by gradient descent.
• Advantages of Autorgressive Viewpoint: Our framework leverages advances in autoregressive generative models (like transformers), allowing for scalability and integration with rich feature representations (e.g., article headlines).

Empirical Evaluation:

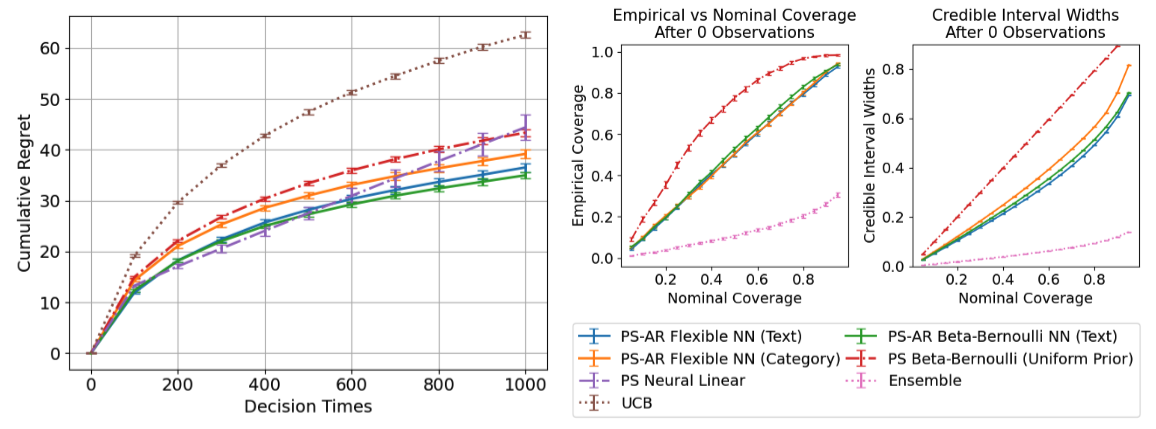
We demonstrate our method on both synthetic and real-world news recommendation tasks. Our results show:

• Improved decision-making: Our approach outperforms traditional bandit algorithms by taking advantage of rich action features like article headlines.
• Uncertainty quantification: Our method allows us to effectively model uncertainty in the mean reward for each article. We use our pretrained sequence model to construct credible intervals for the mean rewards and find they have extremely well calibrated coverage.

Left: In terms of cumulative regret, the PS-AR models that use sequence models $p_\theta$ that incorporate text features outperform all other algorithms. Right: We form credible intervals for the mean reward for each article/action by autoregressively sampling (imputing) many hypothetical sequences of future rewards given the article headline.